Normaaljaotus

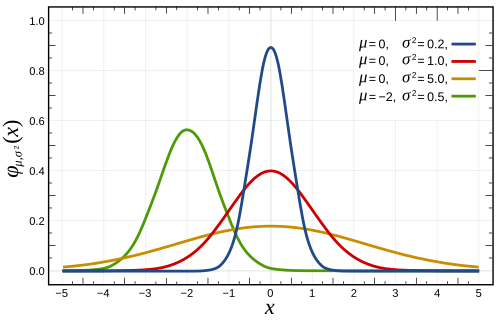
Normaaljaotuseks (ka Gaussi jaotuseks) nimetatakse matemaatikas pideva juhusliku suuruse X jaotust, mida iseloomustab tihedusfunktsioon^[1]

${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}$

kus

• ${\displaystyle \mu }$ on keskväärtus, mis iseloomustab kõige suurema tõenäosusega esinevat suurust (normaaljaotusel sama väärtusega ka aritmeetiline keskmine, mediaan ja mood);
• ${\displaystyle \sigma }$ on standardhälve, mis iseloomustab, kui palju juhuslikud suurused keskväärtusest erinevad. Normaaljaotuse tihedusfunktsiooni nimetatakse ka Gaussi funktsiooniks ja selle graafikut Gaussi kõveraks.

Normaaljaotuse eriline tähtsus tuleneb tsentraalsest piirteoreemist, mille kohaselt suure arvu sõltumatute muutujate liitmisel, on nõrkadel eeldustel saadud jaotus ligilähedaselt normaaljaotus.

Paljude mõõtmistulemuste hälbeid keskmisest saab loodus-, majandus- ja tehnikateadustes kas täpselt või väga heas lähenduses kirjeldada normaaljaotuse (bioloogias sageli logaritmilise normaaljaotuse) abil. See on nii eeskätt olukordades, kus paljud faktorid mõjuvad üksteisest sõltumatult eri suundades.